Description:
The focus of the test is the proportion of zeroes and ones for the entire sequence. The purpose of this test is to determine whether that number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to ½, that is, the number of ones and zeroes in a sequence should be about the same.
Process
1. Program convert zeros to -1, and add them all into a single variable, which we will call Sn.
2. We perform the following statistics:
3. Calculate P - value as follows:
Program:
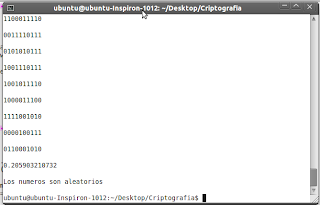
Result
Bibliography:
http://www.random.org/statistics/frequency-monobit/
http://csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html
jueves, 30 de agosto de 2012
martes, 28 de agosto de 2012
Aplicaciones de logica proposicional
¿Que es logica proposicionl?
 La lógica proposicional es la más antigua y simple de las formas de
lógica, es la parte que permite el razonamiento, a través de un
mecanismo que primero evalúa sentencias simples y luego sentencias
complejas, formadas mediante el uso de conectivos proposicionales, por
ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una
sentencia compleja, analizando los valores de veracidad asignados a las
sentencias simples que la conforman.
La lógica proposicional es la más antigua y simple de las formas de
lógica, es la parte que permite el razonamiento, a través de un
mecanismo que primero evalúa sentencias simples y luego sentencias
complejas, formadas mediante el uso de conectivos proposicionales, por
ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una
sentencia compleja, analizando los valores de veracidad asignados a las
sentencias simples que la conforman.
Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
Una proposición es una sentencia simple que tiene un valor asociado ya sea de verdadero (V), o falso (F). Por ejemplo:
Los conectadores básicos de la lógica proposicional, se dan en la siguiente tabla
Límites de la lógica proposicional
La maquinaria de la lógica proposicional permite formalizar y teorizar sobre la validez de una gran cantidad de argumentos. Sin embargo, también existen argumentos que son intuitivamente válidos, pero cuya validez no puede ser probada por la lógica proposicional. Por ejemplo, considérese el siguiente argumento:
Como este argumento no contiene ninguna de las conectvias «no», «y», «o», etc., según la lógica proposicional, su formalización será la siguiente:
Pero esta es una forma de argumento inválida, y eso contradice nuestra intuición de que el argumento es válido. Para teorizar sobre la validez de este tipo de argumentos, se necesita investigar la estructura interna de las variables proposicionales. De esto se ocupa la lógica de primer orden.
Aplicaciones de la logica proposicional
Existen muchas aplicaciones de la logica proposicional aqui menciono algunas y explicare dos ejemplos sobre que tratan.
Problema de los veraces y los mentirosos
Enunciado: En una isla hay dos tribus, la de los veraces (que siempre dicen la verdad) y la de los mentirosos (que siempre mienten). Un viajero se encuentra con tres isleños A, B y C y cada uno le dice una frase:
Representación:
El problema de las 4 reinas
Enunciado: Calcular las formas de colocar 4 reinas en un tablero de 4x4 de forma que no haya más de una reina en cada fila, columna o diagonal.
Representación: cij (1 ≤ i, j ≤ 4) indica que hay una reina en la
fila i columna j.
Logica proposicional en inteligencia artificial
La lógica proposicional toma un rol muy importante en el desarrollo de la inteligencia artificial.
HIPÓTESIS DE LA REPRESENTACIÓN DEL CONOCIMIENTO
Una visión muy frecuente (Aunque es controversial) entre los investigadores de la Inteligencia Artificial es que para que un sistema sea "artificial inteligente," debe contener un Componente que se puede entender como lingüístico (es decir, que puede ser expresado en algún lenguaje)
tales que:
Un Agente Basado en Conocimiento (ABC) es aquel sistema que posee conocimiento de su mundo y que es capaz de razonar sobre las posibles acciones que puede tomar para cambiar el estado de su mundo.
El ABC es un conjunto de sentencias, representado mediante un lenguaje de representación de conocimiento.
EL ABC consiste principalmente en:
Base del conocimiento:
Es un sistema de oraciones que representan hechos acerca del mundo, expresado en un algún lenguaje de representación del conocimiento.
Cada hecho está representado por una sentencia u oración
Siempre que se ejecuta el programa del agente basado en el conocimiento, sucede dos cosas:
Motor de inferencia
Deduce nuevas oraciones o sentencias a partir de las oraciones almacenadas en la base de conocimiento y de las nuevas percepciones
Adición de nuevo conocimiento
Bibliografias:
http://www.monografias.com/trabajos/iartificial/pagina4_1.htm
http://es.wikipedia.org/wiki/L%C3%B3gica_proposicional
aplicaciones: www.cs.us.es/~jalonso/cursos/li/temas/tema-14.pdf
aplicacion IA: http://www.monografias.com/trabajos51/inteligencia-artificial/inteligencia-artificial.shtml
 La lógica proposicional es la más antigua y simple de las formas de
lógica, es la parte que permite el razonamiento, a través de un
mecanismo que primero evalúa sentencias simples y luego sentencias
complejas, formadas mediante el uso de conectivos proposicionales, por
ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una
sentencia compleja, analizando los valores de veracidad asignados a las
sentencias simples que la conforman.
La lógica proposicional es la más antigua y simple de las formas de
lógica, es la parte que permite el razonamiento, a través de un
mecanismo que primero evalúa sentencias simples y luego sentencias
complejas, formadas mediante el uso de conectivos proposicionales, por
ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una
sentencia compleja, analizando los valores de veracidad asignados a las
sentencias simples que la conforman. Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
Una proposición es una sentencia simple que tiene un valor asociado ya sea de verdadero (V), o falso (F). Por ejemplo:
- Hoy es martes
- Hace frío
- hoy_es_martes
- hace_frío
- hoy_es_martes y hace_frío.
Los conectadores básicos de la lógica proposicional, se dan en la siguiente tabla
NOMBRE
|
CONECTOR
|
SÍMBOLO
|
| Conjunción Disyunción Negación Implicación Equivalencia |
AND
OR
NOT
If-Then
Igual
|
^
v
~
=>
=
|
Límites de la lógica proposicional
La maquinaria de la lógica proposicional permite formalizar y teorizar sobre la validez de una gran cantidad de argumentos. Sin embargo, también existen argumentos que son intuitivamente válidos, pero cuya validez no puede ser probada por la lógica proposicional. Por ejemplo, considérese el siguiente argumento:
- Todos los hombres son mortales.
- Sócrates es un hombre.
- Por lo tanto, Sócrates es mortal.
Como este argumento no contiene ninguna de las conectvias «no», «y», «o», etc., según la lógica proposicional, su formalización será la siguiente:
- p
- q
- Por lo tanto, r
Pero esta es una forma de argumento inválida, y eso contradice nuestra intuición de que el argumento es válido. Para teorizar sobre la validez de este tipo de argumentos, se necesita investigar la estructura interna de las variables proposicionales. De esto se ocupa la lógica de primer orden.
Aplicaciones de la logica proposicional
Existen muchas aplicaciones de la logica proposicional aqui menciono algunas y explicare dos ejemplos sobre que tratan.
- El problema de los veraces y los mentirosos
- El problema de los animales
- El problema de los trabajos
- El problema de los cuadrados
- El problema del coloreado del pentágono
- El problema del palomar
- El problema de los rectángulos
- El problema de las 4 reinas
- El problema de Ramsey
- Comparación de los problemas
Problema de los veraces y los mentirosos
Enunciado: En una isla hay dos tribus, la de los veraces (que siempre dicen la verdad) y la de los mentirosos (que siempre mienten). Un viajero se encuentra con tres isleños A, B y C y cada uno le dice una frase:
- A dice “B y C son veraces syss C es veraz”
- B dice “Si A y B son veraces, entonces B y C son veraces y A es mentiroso”
- C dice “B es mentiroso syss A o B es veraz”
Representación:
- a, b y c representan que A, B y C son veraces
- -a, -b y -c representan que A, B y C son mentirosos
El problema de las 4 reinas
Enunciado: Calcular las formas de colocar 4 reinas en un tablero de 4x4 de forma que no haya más de una reina en cada fila, columna o diagonal.
Representación: cij (1 ≤ i, j ≤ 4) indica que hay una reina en la
fila i columna j.
Logica proposicional en inteligencia artificial
La lógica proposicional toma un rol muy importante en el desarrollo de la inteligencia artificial.
HIPÓTESIS DE LA REPRESENTACIÓN DEL CONOCIMIENTO
Una visión muy frecuente (Aunque es controversial) entre los investigadores de la Inteligencia Artificial es que para que un sistema sea "artificial inteligente," debe contener un Componente que se puede entender como lingüístico (es decir, que puede ser expresado en algún lenguaje)
tales que:
- Este componente contiene el conocimiento del sistema, y
- Este componente conduce el comportamiento inteligente del sistema
Un Agente Basado en Conocimiento (ABC) es aquel sistema que posee conocimiento de su mundo y que es capaz de razonar sobre las posibles acciones que puede tomar para cambiar el estado de su mundo.
El ABC es un conjunto de sentencias, representado mediante un lenguaje de representación de conocimiento.
EL ABC consiste principalmente en:
Base del conocimiento:
Es un sistema de oraciones que representan hechos acerca del mundo, expresado en un algún lenguaje de representación del conocimiento.
Cada hecho está representado por una sentencia u oración
Siempre que se ejecuta el programa del agente basado en el conocimiento, sucede dos cosas:
- El programa informa a la Base de Conocimiento lo que percibe.
- El programa pregunta a la Base de Conocimiento qué hacer, luego graba la respuesta.
- La pregunta se responde mediante el razonamiento lógico.
Motor de inferencia
Deduce nuevas oraciones o sentencias a partir de las oraciones almacenadas en la base de conocimiento y de las nuevas percepciones
Adición de nuevo conocimiento
Bibliografias:
http://www.monografias.com/trabajos/iartificial/pagina4_1.htm
http://es.wikipedia.org/wiki/L%C3%B3gica_proposicional
aplicaciones: www.cs.us.es/~jalonso/cursos/li/temas/tema-14.pdf
aplicacion IA: http://www.monografias.com/trabajos51/inteligencia-artificial/inteligencia-artificial.shtml
jueves, 23 de agosto de 2012
Laboratorio ejercicio 1: Tutorial gnuplot
Gnuplot es un programa en línea de comandos que permite dibujar gráficas de funciones en 2 y 3 dimensiones a través de las fórmulas que las definen. También puede dibujar gráficos usando una tabla de coordenadas (en formato sólo texto) creadas con cualquier programa.
El software tiene copyright pero se distribuye libremente y está disponible para UNIX, Linux, IBM OS/2, MS Windows, MSDOS, Macintosh, VMS, Atari y muchas otras plataformas.
Originalmente estaba destinado a científicos y estudiantes para permitirles visualizar gráficamente funciones matemáticas o tablas de datos. Hace su trabajo muy bien y es utilizado por otras herramientas, entre las que se encuentran Maxima y Octave, para dibujar gráficas evitandoles tener que desarrollar su propio motor de dibujo (un ejemplo paradigmático de software libre y cooperativo).
Gnuplot viene desarrollándose desde 1986 y la última versión, es la 4.4.4 y está fechada el 3 de marzo de 2007.
Además de dibujar la gráfica en pantalla puede guardarla en multitud de formatos entre los que se encuentran los usuales, como jpg, png, pdf, svg; y otros, menos usuales, pero muy interesantes para los usuarios LaTeX como metafont, eps, pstricks, picture.
Instalación
Como ya se sabe la sencillez para instalar en ubuntu (linux). Para instalar, ejecutamos el siguiente comando:
$ sudo apt-get install gnuplot
Ejecución
Sólo ejecuta gnuplot, verás que te despliega un mensaje (versión, créditos, un poco de ayuda) en pantalla:
$ gnuplot
Ayuda en línea
Una vez entremos en modo interactivo, gnuplot dispone de un completísimo manual interactivo que se accede mediante el comando help al que bastará con dar cualquier nombre de comando para que nos explique su funcionamiento y opciones. Para salir del modo interactivo tenemos dos comandos equivalentesexit y quit.
En general, cualquier expresión matemática aceptada por los lenguajes de programación más comunes como C, FORTRAN, PASCAL o BASIC es válida. Los espacios en blanco son ignorados y la precedencia de los operadores es como en C o FORTRAN. Acepta números complejos que deben escribirse en la forma {3,2} = 3 + 2i, en esta forma {0,1} representa al propio i. Las funciones de gnuplot son las mismas de la librería matemática UNIX (las mismas que utiliza el FORTRAN).
Los comandos primarios del programa son plot y splot. Ellos dibujan funciones y datos de muchísimas formas posibles. plot se utiliza para gráficos en 2-d (variables x, y) y splot se utiliza para gráficos en 3-d (variables x, y, z). Una explicación detallada de estos comandos puede obtenerse mediante:
gnuplot> help plot
gnuplot> help splot
La sintaxis general para representar graficas 2-d de funciones de una variable es:
donde se pone el nombre de la < función> que queremos representar o el nombre del < fichero-de-datos> , entre comillas (simples o dobles), con los datos num ́ricos de las e coordenadas a representar.
Grafica funciones simples
¿Qué tal graficar funciones trigonométricas básicas? Puedes poner todas en una sola figura únicamente separándolas con comas. Los rangos pueden especificarse entre corchetes cuadrados. La letra “x” será tomada como variable de referencia para gnuplot. Al ejecutar el comando te aparecerá una ventana con la gráfica de cada función; desde la que podrás, entre otras cosas, salvar la gráfica en el portapapeles.
gnuplot> plot [-10:10] sin(x), atan(x), cos(atan(x))
Así puedes ver la lista de funciones soportadas:
gnuplot> help functions
Cambia las opciones por defecto
Por defecto, cada función aparece diferenciada por un color, todas con el mismo tipo y grosor de línea, con una leyenda y enmarcadas por los ejes X y Y. Por supuesto, cada una de estas opciones puede modificarse. Veamos como modificar todas a partir del ejemplo anterior y sólo para la función sin(x).
Establecemos el título de la gráfica con title.
gnuplot> set title "Funciones trigonométricas"
Un comando importante es set ya que con él pueden modificarse los gráficos de plot y splot. Los comandos set crean y configura el ambiente de trabajo sobre el cual trabajara la aplicación. El comando set controla casi todos los parámetros de la curva. Tiene multitud de variantes que pueden verse con help set Se incluye entre estos controles la opción de modificar los ejes. Así:
gnuplot>set xrange [xmin:xmax]
gnuplot>set yrange [xmin:xmax]
para ver mas sobre el comando set pueden teclear:
gnuplot>set help
Establecemos los nombres de los ejes X y Y con xlabel y ylabel.
gnuplot> set xlabel "x [grados]"
gnuplot> set ylabel "y(x)"
Establecemos leyenda (title), línea punteada (linespoints), color (linetype), y grosor (linewidth) a sin(x).
gnuplot> plot [-pi:pi] sin(x) title "sen(x)" with linespoints linetype 4 linewidth 3, atan(x), cos(atan(x))
Cada opción tiene versión corta. Con esto, el comando anterior queda así:
gnuplot> plot [-pi:pi] sin(x) t "sen(x)" w lp lt 4 lw 3, atan(x), cos(atan(x))
Notemos que la función sin(x) aparece con color violeta, mayor grosor y con puntos en la línea.
Hay muchas opciones para el estilo al dibujar los datos
Grafica datos
Gnuplot trabaja de manera natural con los datos. Supongamos que tienes un archivo “experimento.dat” con un montón de datos dispuestos en dos columnas. Graficar esos datos es tan sencillo como esto:
gnuplot> plot "experimento.dat"
Como podemos ver esta grafica nos imprimio los nombres de la grafica anterior, como solucionamos esto?, solamente tecleamos esto:
gnuplot> reset
Como pueden ver la grafica queda limpia y sin los nombres que le habiamos dado.
Toma en cuenta que el archivo con los datos debe estar en el mismo directorio desde donde ejecutaste gnuplot. De lo contrario, debes indicar, entre comillas, la ruta completa. También considera que la primera y segunda columna del archivo serán los ejes X y Y, respectivamente.
¿Se puede dibujar una sola columna de esos datos? Claro que sí, dibujaremos solamente la columna primera y segunda de los datos del archivo "experimentos.dat"
Para realizar esto debemos ejecutar esta secuencia de comandos:
gnuplot>set style data lines
gnuplot>plot 'experimentos.dat' using 1:2
El comando using especifíca la columna que será dibujada, si los datos están en 3 columnas, hay muchas posibilidades de dibujar, por ejemplo al usar... using 3:2 se dibujará la columna 3 en el primer eje X y la columna 2 en el segundo eje Y.
Si necesitáramos hacer operaciones con los datos de una o algunas columnas y esos resultados graficarlos como otra columna, es posible hacerlo en gnuplot. Bueno, hay varias maneras de hacerlo, una de ellas es hacer las operaciones en otro programa como una hoja de cálculo. Pero, la manera más fácil (si ya se tiene gnuplot ) es usar esas capacidades que se incorporaron desde la versión 3.7. Vamos a suponer por ahora que el archivo 'experimentos.dat' contiene los datos de las componenetes x, y, z de la velocidad que es la que queremos dibujar. La velocidad está determinada mediante la expresión
La manera de hacerlo en gnuplot es calcular esa velocidad como:
gnuplot> plot 'experimientos.dat' \
> using (sqrt($1**2+$2**2+$3**2))
Note que la línea diagonal \ nos permite escribir en el siguiente renglón, y el comando se ejecutará hasta después de haber pulsado enter. También hay que notar que las columnas se especifican con $1, o $2, o $3 y las potencias con **, como por ejemplo 3^2 así se escribe en gnuplot como 3**2. Note que los paréntesis que acotan la expresión son importantes.
Para graficar una función 3D, debes utilizar el comando splot. Los rangos se definen aparte.
El rango en X.
gnuplot> set xrange [-2:2]
El rango en Y.
gnuplot> set yrange [-2:2]
Usando splot y con exp, el exponente de -x que multiplica a x
gnuplot> splot exp(-x * x) * exp(-y * y)
Para salir de gnuplot utilizamos:
gnuplot>exit
Pequeño ejemplo en python:
Para hacer funcionar python-gnuplot, primero tenemos que instalarlo, nos iremos a synaptic package manager de ubuntu y lo buscaremos de esta manera python-gnuplot. Para que la libreria import gnuplot pueda funcionar sin problema al compilar.
programa sencillo:
Bibliografias
Esta pagina ayudara mucho a enteder lo que estoy explicando.
http://computacion.cs.cinvestav.mx/~acaceres/courses/gnuplotCurso/node3.html
Aqui encontraran mas funciones sobre gnuplot
http://gnuplot.sourceforge.net/demo_4.2/
El software tiene copyright pero se distribuye libremente y está disponible para UNIX, Linux, IBM OS/2, MS Windows, MSDOS, Macintosh, VMS, Atari y muchas otras plataformas.
Originalmente estaba destinado a científicos y estudiantes para permitirles visualizar gráficamente funciones matemáticas o tablas de datos. Hace su trabajo muy bien y es utilizado por otras herramientas, entre las que se encuentran Maxima y Octave, para dibujar gráficas evitandoles tener que desarrollar su propio motor de dibujo (un ejemplo paradigmático de software libre y cooperativo).
Gnuplot viene desarrollándose desde 1986 y la última versión, es la 4.4.4 y está fechada el 3 de marzo de 2007.
Además de dibujar la gráfica en pantalla puede guardarla en multitud de formatos entre los que se encuentran los usuales, como jpg, png, pdf, svg; y otros, menos usuales, pero muy interesantes para los usuarios LaTeX como metafont, eps, pstricks, picture.
Instalación
Como ya se sabe la sencillez para instalar en ubuntu (linux). Para instalar, ejecutamos el siguiente comando:
$ sudo apt-get install gnuplot
Ejecución
Sólo ejecuta gnuplot, verás que te despliega un mensaje (versión, créditos, un poco de ayuda) en pantalla:
$ gnuplot
Ayuda en línea
Una vez entremos en modo interactivo, gnuplot dispone de un completísimo manual interactivo que se accede mediante el comando help al que bastará con dar cualquier nombre de comando para que nos explique su funcionamiento y opciones. Para salir del modo interactivo tenemos dos comandos equivalentesexit y quit.
En general, cualquier expresión matemática aceptada por los lenguajes de programación más comunes como C, FORTRAN, PASCAL o BASIC es válida. Los espacios en blanco son ignorados y la precedencia de los operadores es como en C o FORTRAN. Acepta números complejos que deben escribirse en la forma {3,2} = 3 + 2i, en esta forma {0,1} representa al propio i. Las funciones de gnuplot son las mismas de la librería matemática UNIX (las mismas que utiliza el FORTRAN).
Los comandos primarios del programa son plot y splot. Ellos dibujan funciones y datos de muchísimas formas posibles. plot se utiliza para gráficos en 2-d (variables x, y) y splot se utiliza para gráficos en 3-d (variables x, y, z). Una explicación detallada de estos comandos puede obtenerse mediante:
gnuplot> help plot
gnuplot> help splot
La sintaxis general para representar graficas 2-d de funciones de una variable es:
plot {rangos} {<funcion> | {"<fichero-de-datos>" {using ...}}}
{titulo} {estilo} {, <funcion> {titulo} {estilo}...}
donde se pone el nombre de la < función> que queremos representar o el nombre del < fichero-de-datos> , entre comillas (simples o dobles), con los datos num ́ricos de las e coordenadas a representar.
Grafica funciones simples
¿Qué tal graficar funciones trigonométricas básicas? Puedes poner todas en una sola figura únicamente separándolas con comas. Los rangos pueden especificarse entre corchetes cuadrados. La letra “x” será tomada como variable de referencia para gnuplot. Al ejecutar el comando te aparecerá una ventana con la gráfica de cada función; desde la que podrás, entre otras cosas, salvar la gráfica en el portapapeles.
gnuplot> plot [-10:10] sin(x), atan(x), cos(atan(x))
Así puedes ver la lista de funciones soportadas:
gnuplot> help functions
Cambia las opciones por defecto
Por defecto, cada función aparece diferenciada por un color, todas con el mismo tipo y grosor de línea, con una leyenda y enmarcadas por los ejes X y Y. Por supuesto, cada una de estas opciones puede modificarse. Veamos como modificar todas a partir del ejemplo anterior y sólo para la función sin(x).
Establecemos el título de la gráfica con title.
gnuplot> set title "Funciones trigonométricas"
Un comando importante es set ya que con él pueden modificarse los gráficos de plot y splot. Los comandos set crean y configura el ambiente de trabajo sobre el cual trabajara la aplicación. El comando set controla casi todos los parámetros de la curva. Tiene multitud de variantes que pueden verse con help set Se incluye entre estos controles la opción de modificar los ejes. Así:
gnuplot>set xrange [xmin:xmax]
gnuplot>set yrange [xmin:xmax]
para ver mas sobre el comando set pueden teclear:
gnuplot>set help
Establecemos los nombres de los ejes X y Y con xlabel y ylabel.
gnuplot> set xlabel "x [grados]"
gnuplot> set ylabel "y(x)"
Establecemos leyenda (title), línea punteada (linespoints), color (linetype), y grosor (linewidth) a sin(x).
gnuplot> plot [-pi:pi] sin(x) title "sen(x)" with linespoints linetype 4 linewidth 3, atan(x), cos(atan(x))
Cada opción tiene versión corta. Con esto, el comando anterior queda así:
gnuplot> plot [-pi:pi] sin(x) t "sen(x)" w lp lt 4 lw 3, atan(x), cos(atan(x))
Notemos que la función sin(x) aparece con color violeta, mayor grosor y con puntos en la línea.
Hay muchas opciones para el estilo al dibujar los datos
|
Grafica datos
Gnuplot trabaja de manera natural con los datos. Supongamos que tienes un archivo “experimento.dat” con un montón de datos dispuestos en dos columnas. Graficar esos datos es tan sencillo como esto:
gnuplot> plot "experimento.dat"
Como podemos ver esta grafica nos imprimio los nombres de la grafica anterior, como solucionamos esto?, solamente tecleamos esto:
gnuplot> reset
Como pueden ver la grafica queda limpia y sin los nombres que le habiamos dado.
Toma en cuenta que el archivo con los datos debe estar en el mismo directorio desde donde ejecutaste gnuplot. De lo contrario, debes indicar, entre comillas, la ruta completa. También considera que la primera y segunda columna del archivo serán los ejes X y Y, respectivamente.
¿Se puede dibujar una sola columna de esos datos? Claro que sí, dibujaremos solamente la columna primera y segunda de los datos del archivo "experimentos.dat"
Para realizar esto debemos ejecutar esta secuencia de comandos:
gnuplot>set style data lines
gnuplot>plot 'experimentos.dat' using 1:2
El comando using especifíca la columna que será dibujada, si los datos están en 3 columnas, hay muchas posibilidades de dibujar, por ejemplo al usar... using 3:2 se dibujará la columna 3 en el primer eje X y la columna 2 en el segundo eje Y.
Si necesitáramos hacer operaciones con los datos de una o algunas columnas y esos resultados graficarlos como otra columna, es posible hacerlo en gnuplot. Bueno, hay varias maneras de hacerlo, una de ellas es hacer las operaciones en otro programa como una hoja de cálculo. Pero, la manera más fácil (si ya se tiene gnuplot ) es usar esas capacidades que se incorporaron desde la versión 3.7. Vamos a suponer por ahora que el archivo 'experimentos.dat' contiene los datos de las componenetes x, y, z de la velocidad que es la que queremos dibujar. La velocidad está determinada mediante la expresión
La manera de hacerlo en gnuplot es calcular esa velocidad como:
gnuplot> plot 'experimientos.dat' \
> using (sqrt($1**2+$2**2+$3**2))
Note que la línea diagonal \ nos permite escribir en el siguiente renglón, y el comando se ejecutará hasta después de haber pulsado enter. También hay que notar que las columnas se especifican con $1, o $2, o $3 y las potencias con **, como por ejemplo 3^2 así se escribe en gnuplot como 3**2. Note que los paréntesis que acotan la expresión son importantes.
Para graficar una función 3D, debes utilizar el comando splot. Los rangos se definen aparte.
El rango en X.
gnuplot> set xrange [-2:2]
El rango en Y.
gnuplot> set yrange [-2:2]
Usando splot y con exp, el exponente de -x que multiplica a x
gnuplot> splot exp(-x * x) * exp(-y * y)
Para salir de gnuplot utilizamos:
gnuplot>exit
Pequeño ejemplo en python:
Para hacer funcionar python-gnuplot, primero tenemos que instalarlo, nos iremos a synaptic package manager de ubuntu y lo buscaremos de esta manera python-gnuplot. Para que la libreria import gnuplot pueda funcionar sin problema al compilar.
programa sencillo:
Bibliografias
Esta pagina ayudara mucho a enteder lo que estoy explicando.
http://computacion.cs.cinvestav.mx/~acaceres/courses/gnuplotCurso/node3.html
Aqui encontraran mas funciones sobre gnuplot
http://gnuplot.sourceforge.net/demo_4.2/
martes, 21 de agosto de 2012
Tautologia
Primero que nada vamos a ver que es una tautologia:
Es una fórmula bien formada de un sistema de lógica proposicional que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad que se haga a sus fórmulas atómicas. La construcción de una tabla de verdad es un método efectivo para determinar si una fórmula cualquiera es una tautología o no.
Por lo tanto, para determinar si una fórmula cualquiera es una tautología, basta con considerar todas las posibles interpretaciones de las fórmulas atómicas, y calcular el valor de verdad del todo. Esto se logra mediante una tabla de verdad.
Ejercicio:
Esta tarea consistia en elaborar una tautologia con las siguientes condiciones:
- 3 variables
- 4 conectivos lógicos
- Por lo menos 1 disyunción, 1 conjunción y 1 negación
1 = falso
0 = verdadero
Aqui el arbol:
Suscribirse a:
Comentarios (Atom)