Description:
The focus of the test is the proportion of zeroes and ones for the entire sequence. The purpose of this test is to determine whether that number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to ½, that is, the number of ones and zeroes in a sequence should be about the same.
Process
1. Program convert zeros to -1, and add them all into a single variable, which we will call Sn.
2. We perform the following statistics:
3. Calculate P - value as follows:
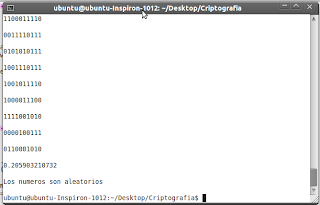
Program:
Result
Bibliography:
http://www.random.org/statistics/frequency-monobit/
http://csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html


Just one test :( 5 pts.
ResponderEliminar