This code is only to encrypt the image
Here the code:
Mostrando entradas con la etiqueta Seguridad de la información y criptografía. Mostrar todas las entradas
Mostrando entradas con la etiqueta Seguridad de la información y criptografía. Mostrar todas las entradas
jueves, 1 de noviembre de 2012
jueves, 25 de octubre de 2012
Extra points
what will be done with this problem is to know if a group with the theory of gruop.
Problem to solve
2 + 3 = 10
8 + 4 = 96
7 + 2 = 63
6 + 5 = 66
9 + 5 = ?
Solution to problem:
2 + 3 = 10 (2+3=5(2))
8 + 4 = 96 (8+4=12(8))
7 + 2 = 63 (7+2=9(7))
6 + 5 = 66 (6+5=11(6))
9 + 5 = ? (9+5=14(9))
Result:
9 + 5 = 126
Associativity:

this point is not met and the order matters of factors in this problem, the result is not the same.
Neutral element:

This time this point is not met because the result set given in the problem are not equal to the sum of any factor.
Symmetrical element:

At this point I think it's obviously not apply to what is being done on the problem
Group:
A group is a set G which has defined an internal composition law that satisfies the above axioms.
Then this, problem is not a group because don´t meets with some requeriments, do as explain his definition.
This is of wikipedia now i try explain of the pdf of Elisa Schaeffer:
Identity:
e°g = g°e = g
this is not true since we have to
a(a + b) = c
a(a + e) is different from c
Reverse:
so if there is no identity, can not be reversed and also used "e"
Associativity:
the associativity is not because we
a (a + b) = c
Not the same that
b (b + a) = c
Closing:
this point is correct because it says that if g ° h belongs to G
And that g, h belongs to G
Are integers
If you multiply
You get a whole number
Then we come to the same conclusion on this problem is not a group
Well, I hope that the result is the desired and sorry for my bad english.
References:
http://es.wikipedia.org/wiki/Teor%C3%ADa_de_grupos
Problem to solve
2 + 3 = 10
8 + 4 = 96
7 + 2 = 63
6 + 5 = 66
9 + 5 = ?
Solution to problem:
2 + 3 = 10 (2+3=5(2))
8 + 4 = 96 (8+4=12(8))
7 + 2 = 63 (7+2=9(7))
6 + 5 = 66 (6+5=11(6))
9 + 5 = ? (9+5=14(9))
Result:
9 + 5 = 126
Associativity:
this point is not met and the order matters of factors in this problem, the result is not the same.
Neutral element:
This time this point is not met because the result set given in the problem are not equal to the sum of any factor.
Symmetrical element:
At this point I think it's obviously not apply to what is being done on the problem
Group:
A group is a set G which has defined an internal composition law that satisfies the above axioms.
Then this, problem is not a group because don´t meets with some requeriments, do as explain his definition.
This is of wikipedia now i try explain of the pdf of Elisa Schaeffer:
Identity:
e°g = g°e = g
this is not true since we have to
a(a + b) = c
a(a + e) is different from c
Reverse:
so if there is no identity, can not be reversed and also used "e"
Associativity:
the associativity is not because we
a (a + b) = c
Not the same that
b (b + a) = c
Closing:
this point is correct because it says that if g ° h belongs to G
And that g, h belongs to G
Are integers
If you multiply
You get a whole number
Then we come to the same conclusion on this problem is not a group
Well, I hope that the result is the desired and sorry for my bad english.
References:
http://es.wikipedia.org/wiki/Teor%C3%ADa_de_grupos
Panama Stream cipher
Introduction:
Panama is a cryptography primitive which can be used both as a hash function and a stream cipher. Based on StepRightUp, it was designed by Joan Daemen and Craig Clapp and presented in the paper Fast Hashing and Stream Encryption with PANAMA on the Fast Software Encryption (FSE) conference 1998. The cipher has influenced several other designs, for example MUGI.
The primitive can be used both as a hash function and a stream cipher. The stream cipher uses a 256-bit key and the performance of the cipher is very good reaching 2 cycles per byte.
As a hash function, collisions have been shown by Vincent Rijmen et al. in the paper Producing Collisions for PANAMA presented at FSE 2001. The attack shows a computational complexity of 2^82 and with negligible memory requirements.
At FSE 2007, Joan Daemen and Gilles Van Assche presented a practical attack on the Panama hash function that generates a collision in 2^6 evaluations of the state updating function.
Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche proposed, at NIST's 2006 Second Cryptographic Hash Workshop, unveiled a Panama variant called RadioGatún. RadioGatún is strictly a hash function; it does not have the known weaknesses that Panama's hash function has.
Structure of Panama
Panama contains two main elements. A shift register, with 32 cells, each containing a vector with eight 32-bit words, and a recirculating mixing function, resembling the f-function in a block cipher, which operates on a "state" consisting of seventeen 32-bit words. (While it has been noted that SHA-1 inspired Panama, I do not find the resemblance obvious.)
There are three fundamental operations that form part of Panama:
When Panama is used as a hash function, the message to be hashed, followed by a 1 bit and as many zeroes as are needed to cause the message to occupy an integer number of 256-bit blocks, is input to Panama through a series of Push operations. Then, after a number of Pull operations with their output discarded, so that the effects of even the last block of the message are fully diffused, the output from a final Pull operation constitutes the hash.
The state transition function of Panama operates on 17 32-bit words, numbered 0 through 16. Its steps are visible in the diagram, and are, in order:
The Panama Stream Encryption Scheme
The stream cipher is initialized by first loading the 256-bit key K, the 256-bit diversification parameter Q, and performing 32 additional blank Pull iterations. During key-stream generation, an eight-word block z is delivered at the output for every iteration. In practice, the diversification parameter allows for frequent resynchronization without the need to change the key.
Vulnerabilities
The first thing to note is that the presence of the blank rounds makes it hard
to produce a collision in the digest if there is a difference in either the state or
the buffer after all the message blocks are input. Due to the invertibility of the
state updating function such a difference will not cancel out. Moreover, the lack
of external input and the propagation properties of the state updating function
give the attacker almost no control over the final difference. Therefore, our goal is to produce a collision in both the state and the buffer before the blank rounds.
We produce a collision by following a trail. Two instances of Panama process
two different messages (p and p + dp), which have a given difference (dp). The
trail also specifies the differences in the state (da) and in the buffer (db) between the two instances of Panama, at each round. So, not only the two messages must have the given difference, they must also produce the right difference in the state and in the buffer.
We shall now describe the general structure of the trail used in the scope of
this article. We will first talk about the sequence of message differences, then
about the differences in the state.
In the sequel, the round numbers are specified between brackets in super-
script: ·(i) . The convention is that p(i) is the message block processed during
round i, and a(i) is the value of the state after round i.
Tracing the path of information through the state transition function of Panama shows that a trivial application of differential cryptanalysis principles does not suffice to obtain some bits of the buffer by means of a known plaintext attack on Panama when used as a stream cipher. The following diagram illustrates what happens when an attack is attempted:
With known plaintext, one knows the value of the output bits from Panama. If one has two successive output blocks from Panama, tracing through the state transition function leads to the following results:
Initially, words 9 through 16 of the state are known.
After the nonlinearity step, words 9 through 14 of the state are still known for certain. The bits of word 15 which correspond to 1 bits in the former value of word 16 are known as well, but the other bits of word 6 are unknown. The bits of word 16 are, with a probability of 75%, the inverses of their former values.
After the bit dispersion step, the words known with certainty are words 2, 4, 9, 11, 14, and 16, and the words about which partial information is available are words 7 and 12. The right words in the right places are not available to allow a known or partly known word to exit the diffusion step for comparison with a word known from the current output block, by which means some buffer contents could be found.
Even so, the fact that it comes this close to solution makes one wary of the danger of a differential attack.
References:
http://en.wikipedia.org/wiki/Panama_(cryptography)
http://www.quadibloc.com/crypto/co4821.htm
http://www.cosic.esat.kuleuven.be/publications/article-81.pdf
Panama is a cryptography primitive which can be used both as a hash function and a stream cipher. Based on StepRightUp, it was designed by Joan Daemen and Craig Clapp and presented in the paper Fast Hashing and Stream Encryption with PANAMA on the Fast Software Encryption (FSE) conference 1998. The cipher has influenced several other designs, for example MUGI.
The primitive can be used both as a hash function and a stream cipher. The stream cipher uses a 256-bit key and the performance of the cipher is very good reaching 2 cycles per byte.
As a hash function, collisions have been shown by Vincent Rijmen et al. in the paper Producing Collisions for PANAMA presented at FSE 2001. The attack shows a computational complexity of 2^82 and with negligible memory requirements.
At FSE 2007, Joan Daemen and Gilles Van Assche presented a practical attack on the Panama hash function that generates a collision in 2^6 evaluations of the state updating function.
Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche proposed, at NIST's 2006 Second Cryptographic Hash Workshop, unveiled a Panama variant called RadioGatún. RadioGatún is strictly a hash function; it does not have the known weaknesses that Panama's hash function has.
Structure of Panama
Panama contains two main elements. A shift register, with 32 cells, each containing a vector with eight 32-bit words, and a recirculating mixing function, resembling the f-function in a block cipher, which operates on a "state" consisting of seventeen 32-bit words. (While it has been noted that SHA-1 inspired Panama, I do not find the resemblance obvious.)
There are three fundamental operations that form part of Panama:
- Panama is reset by setting both the 17-word state and the contents of the shift register to all zeroes.
- A vector of eight 32-bit words is fed to Panama through a Push operation. Operations unique to the Push function are shown by the light dotted lines in the diagram. In a Push operation, the incoming vector is used as one of the inputs to the state transition function (the other input is the contents of one of the cells in the shift register), and is also used to XOR with the recirculating values in the shift register.
- A vector of eight 32-bit words is recieved from Panama by means of a Pull operation. The line of alternating dots and dashes shows the operations unique to the Pull function in the diagram. In a Pull operation, the 32-bit words numbered 9 through 16 in the state are used as the output, and words 1 through 8 are XORed with the recirculating values in the shift register. The inputs to the state transition function both come from stages in the shift register, one not used for any special purpose in the Push operation replacing the input, absent from a Pull operation.
When Panama is used as a hash function, the message to be hashed, followed by a 1 bit and as many zeroes as are needed to cause the message to occupy an integer number of 256-bit blocks, is input to Panama through a series of Push operations. Then, after a number of Pull operations with their output discarded, so that the effects of even the last block of the message are fully diffused, the output from a final Pull operation constitutes the hash.
The state transition function of Panama operates on 17 32-bit words, numbered 0 through 16. Its steps are visible in the diagram, and are, in order:
- Nonlinearity: each word is XORed with the OR of the previous values of the next word and the complement of the word after, going around the circle from word 0 to 16 and back to 0.
- Bit Dispersion: first, the words are transposed (by a simple decimation with interval 4), then the words undergo circular left shifts of different sizes.
- Diffusion: each word is XORed with both the previous values of the next word and the word four positions ahead, again going around the circle.
- Buffer Injection: Word 0 is XORed with 1; words 1 through 8 are XORed with the first input to the function, and words 9 through 16 are XORed with the second input to the function.
The Panama Stream Encryption Scheme
The stream cipher is initialized by first loading the 256-bit key K, the 256-bit diversification parameter Q, and performing 32 additional blank Pull iterations. During key-stream generation, an eight-word block z is delivered at the output for every iteration. In practice, the diversification parameter allows for frequent resynchronization without the need to change the key.
Vulnerabilities
The first thing to note is that the presence of the blank rounds makes it hard
to produce a collision in the digest if there is a difference in either the state or
the buffer after all the message blocks are input. Due to the invertibility of the
state updating function such a difference will not cancel out. Moreover, the lack
of external input and the propagation properties of the state updating function
give the attacker almost no control over the final difference. Therefore, our goal is to produce a collision in both the state and the buffer before the blank rounds.
We produce a collision by following a trail. Two instances of Panama process
two different messages (p and p + dp), which have a given difference (dp). The
trail also specifies the differences in the state (da) and in the buffer (db) between the two instances of Panama, at each round. So, not only the two messages must have the given difference, they must also produce the right difference in the state and in the buffer.
We shall now describe the general structure of the trail used in the scope of
this article. We will first talk about the sequence of message differences, then
about the differences in the state.
In the sequel, the round numbers are specified between brackets in super-
script: ·(i) . The convention is that p(i) is the message block processed during
round i, and a(i) is the value of the state after round i.
Tracing the path of information through the state transition function of Panama shows that a trivial application of differential cryptanalysis principles does not suffice to obtain some bits of the buffer by means of a known plaintext attack on Panama when used as a stream cipher. The following diagram illustrates what happens when an attack is attempted:
With known plaintext, one knows the value of the output bits from Panama. If one has two successive output blocks from Panama, tracing through the state transition function leads to the following results:
Initially, words 9 through 16 of the state are known.
After the nonlinearity step, words 9 through 14 of the state are still known for certain. The bits of word 15 which correspond to 1 bits in the former value of word 16 are known as well, but the other bits of word 6 are unknown. The bits of word 16 are, with a probability of 75%, the inverses of their former values.
After the bit dispersion step, the words known with certainty are words 2, 4, 9, 11, 14, and 16, and the words about which partial information is available are words 7 and 12. The right words in the right places are not available to allow a known or partly known word to exit the diffusion step for comparison with a word known from the current output block, by which means some buffer contents could be found.
Even so, the fact that it comes this close to solution makes one wary of the danger of a differential attack.
References:
http://en.wikipedia.org/wiki/Panama_(cryptography)
http://www.quadibloc.com/crypto/co4821.htm
http://www.cosic.esat.kuleuven.be/publications/article-81.pdf
jueves, 18 de octubre de 2012
Cipher block: Safer
Introduction.
In cryptography, SAFER (Secure And Fast Encryption Routine) is the name of a family of block ciphers designed primarily by James Massey (one of the designers of IDEA) on behalf of Cylink Corporation. The early SAFER K and SAFER SK designs share the same encryption function, but differ in the number of rounds and the key schedule. More recent versions SAFER+ and SAFER++ were submitted as candidates to the AES process and the NESSIE project respectively. All of the algorithms in the SAFER family are unpatented and available for unrestricted use.
A weakness in the key schedule was corrected, with an S being added to the original Safer K designation to create Safer SK. There are some attacks against reduced round variants of Safer. Safer is secure against differential and linear cryptanalysis. However, Bruce Schneier, author of Applied Cryptography, recommends against using Safer because, "Safer was designed for Cylink, and Cylink is tainted by the NSA."
Structure
Description of SAFER
SAFER is a block cipher that operates on 64-bit blocks considered as 8 bytes. It consists of a round transformation iterated r times followed by a final output transformation. Recommended values of r are 6 for SAFER K-64 and 10 for SAFER K-128. The key scheduling, described below, gives (2r + 1) 8-byte subkeys K1; : : : ; K2r+1. Subkeys K2i¡-1 and K2i are used in round i, and the subkey K2r+1 is used in the output transformation. A diagram of the round function is given in the image. The ith round function is built from four basic operations.
1. Mixed XOR/Addition Layer: Bytes 1; 4; 5; 8 of the round input are XORed with bytes 1; 4; 5; 8 of subkey K2i¡-1. Bytes 2; 3; 6; 7 of the round input are added bytewise (modulo 256) with bytes 2; 3; 6; 7 of subkey K2i¡-1.
2. Nonlinear Layer: For a byte x, 45 .x/is defined to be 45x modulo 257, where x is regarded as a number 0 · x · 255, with the convention that 45 .128/ D 0. As 257 is prime and 45 is a primitive element modulo 257, this is an invertible function of a byte, and log 45.¢/ is defined to be its inverse. The 45.¢/transformation is applied to bytes 1; 4; 5; 8 of the output of the mixed XOR=addition layer and the log 45.¢/transformation to bytes 2; 3; 6; 7.
3. Mixed Addition=XOR Layer: Bytes 1; 4; 5; 8 of the output of the nonlinear layer are added bytewise (modulo 256) with bytes 1; 4; 5; 8 of subkey K2i. Bytes 2; 3; 6; 7 of the output of the nonlinear layer are XORed with bytes 2; 3; 6; 7 of subkey K2i.
4. Pseudo-Hadamard Transform (PHT) Layer: The transforms 2-PHT in Fig. 1 map the byte pair .a1; a2/ to the byte pair .2a1 Ca2; a1 Ca2/, where addition is modulo 256. The effect of the three layers of 2-PHT transforms on the output v of the mixed addition=XOR layer is to map it to vM, where addition is modulo 256 and the output of the PHT layer is the output of the round function.
The final output transformation afterr rounds is an application of the mixed XOR/addition layer with the output of the rth round and the subkey K2r+1.
Decryption using SAFER is carried out by reversing these operations and we do not describe it in detail.
Design Principles for SAFER
•Encrypting structure – faster diffusion than for substitution-permutation cipher.
• Byte orientation – during encryption and decryption, all operations are on bytes.
• Group operation at round input – “perfect secrecy” with a “one-time key”.
•Use of 2 additive group operations on bytes -- takes advantage of each’s
strength.
•Confusion via well-defined nonlinear functions – no “suspicious-looking”
tables.
•Fast-diffusing linear transformation – via the PHT and the Armenian shuffle.
•Scalability – Bytes can be made to 2 or 4 (or even 16) bit characters for study.
•Biases in key schedules – eliminates “weak keys”.
•Parity word and selections in key schedules – diversity in round subkeys.
•Number of rounds – chosen for security with a margin of safety.
ANSI C with 200 MHz Pentium Platform: • SAFER+ with 128 bit key (8 rounds) – about 18.2* megabits/s of
encrypted data and about 15.3 microseconds to run the key schedule.
• SAFER+ with 192 bit key (12 rounds) – about 12.3* megabits/s of
encrypted data and about 28.6 microseconds to run the key schedule.
• SAFER+ with 256 bit key (16 rounds) – about 9.3* megabits/s of
encrypted data and about 45.7 microseconds to run the key schedule.
Assembly on 8-bit Processors of the MCS 51 family with 16 MHz clock: •SAFER+ with 128 bit key (8 rounds) – about 25.6 kilobits/s of encrypted data.
• SAFER+ with 192 bit key (12 rounds) – about 16.9 kilobits/s of encrypted data.
• SAFER+ with 256 bit key (16 rounds) – about 12.7 kilobits/s of encrypted data.
Advantages of SAFER+•A proven track record of security
•Speed and simplicity
• Transparency
• Flexibility of Use
• Flexibility of Environment
Limitations of SAFER+ •No proof of complete security
• Encryption/Decryption Dissimilarity
References:
http://tlapixqui.izt.uam.mx/sem_cripto/safer/AnalysisOfSAFER.pdf
http://csrc.nist.gov/archive/aes/round1/conf1/saferpls-slides.pdf
http://en.wikipedia.org/wiki/SAFER
http://kremlinencrypt.com/algorithms.htm
In cryptography, SAFER (Secure And Fast Encryption Routine) is the name of a family of block ciphers designed primarily by James Massey (one of the designers of IDEA) on behalf of Cylink Corporation. The early SAFER K and SAFER SK designs share the same encryption function, but differ in the number of rounds and the key schedule. More recent versions SAFER+ and SAFER++ were submitted as candidates to the AES process and the NESSIE project respectively. All of the algorithms in the SAFER family are unpatented and available for unrestricted use.
A weakness in the key schedule was corrected, with an S being added to the original Safer K designation to create Safer SK. There are some attacks against reduced round variants of Safer. Safer is secure against differential and linear cryptanalysis. However, Bruce Schneier, author of Applied Cryptography, recommends against using Safer because, "Safer was designed for Cylink, and Cylink is tainted by the NSA."
Structure
Description of SAFER
SAFER is a block cipher that operates on 64-bit blocks considered as 8 bytes. It consists of a round transformation iterated r times followed by a final output transformation. Recommended values of r are 6 for SAFER K-64 and 10 for SAFER K-128. The key scheduling, described below, gives (2r + 1) 8-byte subkeys K1; : : : ; K2r+1. Subkeys K2i¡-1 and K2i are used in round i, and the subkey K2r+1 is used in the output transformation. A diagram of the round function is given in the image. The ith round function is built from four basic operations.
1. Mixed XOR/Addition Layer: Bytes 1; 4; 5; 8 of the round input are XORed with bytes 1; 4; 5; 8 of subkey K2i¡-1. Bytes 2; 3; 6; 7 of the round input are added bytewise (modulo 256) with bytes 2; 3; 6; 7 of subkey K2i¡-1.
2. Nonlinear Layer: For a byte x, 45 .x/is defined to be 45x modulo 257, where x is regarded as a number 0 · x · 255, with the convention that 45 .128/ D 0. As 257 is prime and 45 is a primitive element modulo 257, this is an invertible function of a byte, and log 45.¢/ is defined to be its inverse. The 45.¢/transformation is applied to bytes 1; 4; 5; 8 of the output of the mixed XOR=addition layer and the log 45.¢/transformation to bytes 2; 3; 6; 7.
3. Mixed Addition=XOR Layer: Bytes 1; 4; 5; 8 of the output of the nonlinear layer are added bytewise (modulo 256) with bytes 1; 4; 5; 8 of subkey K2i. Bytes 2; 3; 6; 7 of the output of the nonlinear layer are XORed with bytes 2; 3; 6; 7 of subkey K2i.
4. Pseudo-Hadamard Transform (PHT) Layer: The transforms 2-PHT in Fig. 1 map the byte pair .a1; a2/ to the byte pair .2a1 Ca2; a1 Ca2/, where addition is modulo 256. The effect of the three layers of 2-PHT transforms on the output v of the mixed addition=XOR layer is to map it to vM, where addition is modulo 256 and the output of the PHT layer is the output of the round function.
The final output transformation afterr rounds is an application of the mixed XOR/addition layer with the output of the rth round and the subkey K2r+1.
Decryption using SAFER is carried out by reversing these operations and we do not describe it in detail.
Design Principles for SAFER
•Encrypting structure – faster diffusion than for substitution-permutation cipher.
• Byte orientation – during encryption and decryption, all operations are on bytes.
• Group operation at round input – “perfect secrecy” with a “one-time key”.
•Use of 2 additive group operations on bytes -- takes advantage of each’s
strength.
•Confusion via well-defined nonlinear functions – no “suspicious-looking”
tables.
•Fast-diffusing linear transformation – via the PHT and the Armenian shuffle.
•Scalability – Bytes can be made to 2 or 4 (or even 16) bit characters for study.
•Biases in key schedules – eliminates “weak keys”.
•Parity word and selections in key schedules – diversity in round subkeys.
•Number of rounds – chosen for security with a margin of safety.
ANSI C with 200 MHz Pentium Platform: • SAFER+ with 128 bit key (8 rounds) – about 18.2* megabits/s of
encrypted data and about 15.3 microseconds to run the key schedule.
• SAFER+ with 192 bit key (12 rounds) – about 12.3* megabits/s of
encrypted data and about 28.6 microseconds to run the key schedule.
• SAFER+ with 256 bit key (16 rounds) – about 9.3* megabits/s of
encrypted data and about 45.7 microseconds to run the key schedule.
Assembly on 8-bit Processors of the MCS 51 family with 16 MHz clock: •SAFER+ with 128 bit key (8 rounds) – about 25.6 kilobits/s of encrypted data.
• SAFER+ with 192 bit key (12 rounds) – about 16.9 kilobits/s of encrypted data.
• SAFER+ with 256 bit key (16 rounds) – about 12.7 kilobits/s of encrypted data.
Advantages of SAFER+•A proven track record of security
•Speed and simplicity
• Transparency
• Flexibility of Use
• Flexibility of Environment
Limitations of SAFER+ •No proof of complete security
• Encryption/Decryption Dissimilarity
References:
http://tlapixqui.izt.uam.mx/sem_cripto/safer/AnalysisOfSAFER.pdf
http://csrc.nist.gov/archive/aes/round1/conf1/saferpls-slides.pdf
http://en.wikipedia.org/wiki/SAFER
http://kremlinencrypt.com/algorithms.htm
jueves, 20 de septiembre de 2012
week 6: Web service RSA
In this week, we need to aplicated a server web with rsa system
Here the code:
In this code i have a problem with the variables and forever show the message not him, i dont know why :C
here some images
here the page
http://alejandroave.260mb.org/Obed/
Here the code:
In this code i have a problem with the variables and forever show the message not him, i dont know why :C
here some images
http://alejandroave.260mb.org/Obed/
miércoles, 5 de septiembre de 2012
Diffie-hellman protocol
A little introduction:
The Diffie-Hellman cryptographic protocol, one due to Whitfield Diffie and Martin Hellman (Diffie-Hellman Problem-> DHP) is a key establishment protocol between parties who have had no previous contact, using an insecure channel, and anonymously (not authenticated).
It is generally used as a means to agree to be symmetric keys used for encryption of a session (session key establishment). Unauthenticated being, however, provides the basis for various protocols authenticated.
Your safety lies in the extreme difficulty (conjectured, not proven) to compute discrete logarithms in a finite field.
Excercise
Data are:
The formulas are:
So,we had to find
first find y with the following numbers:
first try :(
Y = 9^8 mod 11 = 9x9x9x9x9x9x9x9 mod 11 = 43046721 mod 11 = 3
second try :(
Y = 9^4 mod 11 = 9x9x9x9 mod 11 = 6561 mod 11 = 5
third try :(
Y = 9^9 mod 11 = 9x9x9x9x9x9x9x9x9 mod 11 = 387420489 mod 11 = 5
fourth try :(
Y = 9^10 mod 11 = 9x9x9x9x9x9x9x9x9x9 mod 11 = 3486784401 mod 11 = 1
fifth try :)
Y = 9^6 mod 11 = 9x9x9x9x9x9 mod 11 = 531441 mod 11 = 9
y = 6
then the x:
first try:
X = 9^5 mod 11 = 9x9x9x9x9 mod 11 = 59049 mod 11 = 1
second try:
X = 9^7 mod 11 = 9x9x9x9x9x9x9 mod 11 = 4782969 mod 11 = 4
x = 7
then find k:
k = 4^6 mod 11 = 4096 mod 11 = 4
k = 4
here my calculations:
that's all.
sorry for my bad english
Bibliography:
http://es.wikipedia.org/wiki/Diffie-Hellman
Image
The Diffie-Hellman cryptographic protocol, one due to Whitfield Diffie and Martin Hellman (Diffie-Hellman Problem-> DHP) is a key establishment protocol between parties who have had no previous contact, using an insecure channel, and anonymously (not authenticated).
It is generally used as a means to agree to be symmetric keys used for encryption of a session (session key establishment). Unauthenticated being, however, provides the basis for various protocols authenticated.
Your safety lies in the extreme difficulty (conjectured, not proven) to compute discrete logarithms in a finite field.
Excercise
Data are:
- p = 11
- g = 9
- X = 4
- Y = 9
The formulas are:
- X = (g^x) mod p
- Y = (g^y) mod p
- k = (Y^x) mod p
- k = (X^y) mod p
So,we had to find
- x = ?
- y = ?
- k = ?
first find y with the following numbers:
first try :(
Y = 9^8 mod 11 = 9x9x9x9x9x9x9x9 mod 11 = 43046721 mod 11 = 3
second try :(
Y = 9^4 mod 11 = 9x9x9x9 mod 11 = 6561 mod 11 = 5
third try :(
Y = 9^9 mod 11 = 9x9x9x9x9x9x9x9x9 mod 11 = 387420489 mod 11 = 5
fourth try :(
Y = 9^10 mod 11 = 9x9x9x9x9x9x9x9x9x9 mod 11 = 3486784401 mod 11 = 1
fifth try :)
Y = 9^6 mod 11 = 9x9x9x9x9x9 mod 11 = 531441 mod 11 = 9
y = 6
then the x:
first try:
X = 9^5 mod 11 = 9x9x9x9x9 mod 11 = 59049 mod 11 = 1
second try:
X = 9^7 mod 11 = 9x9x9x9x9x9x9 mod 11 = 4782969 mod 11 = 4
x = 7
then find k:
k = 4^6 mod 11 = 4096 mod 11 = 4
k = 4
here my calculations:
that's all.
sorry for my bad english
Bibliography:
http://es.wikipedia.org/wiki/Diffie-Hellman
Image
jueves, 30 de agosto de 2012
Frequency (Monobits) Test
Description:
The focus of the test is the proportion of zeroes and ones for the entire sequence. The purpose of this test is to determine whether that number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to ½, that is, the number of ones and zeroes in a sequence should be about the same.
Process
1. Program convert zeros to -1, and add them all into a single variable, which we will call Sn.
2. We perform the following statistics:
3. Calculate P - value as follows:
Program:
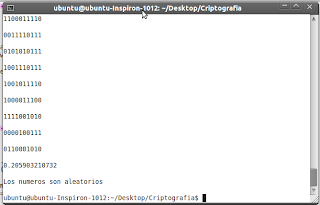
Result
Bibliography:
http://www.random.org/statistics/frequency-monobit/
http://csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html
The focus of the test is the proportion of zeroes and ones for the entire sequence. The purpose of this test is to determine whether that number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to ½, that is, the number of ones and zeroes in a sequence should be about the same.
Process
1. Program convert zeros to -1, and add them all into a single variable, which we will call Sn.
2. We perform the following statistics:
3. Calculate P - value as follows:
Program:
Result
Bibliography:
http://www.random.org/statistics/frequency-monobit/
http://csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html
martes, 7 de agosto de 2012
Suscribirse a:
Entradas (Atom)